2.3 Kirchhoff-Based Localisation - Single component

This tutorial illustrates how to perform source localisation using a Kirchhoff-based modelling operator.

To begin with, we express the process of creating a microseismic recording from a source (or a set of distributed sources) using the following integral relation:

\[d(\mathbf{x_r}, t) = w(t) * \int\limits_V G(\mathbf{x_r}, \mathbf{x}, t) m(\mathbf{x})\,\mathrm{d}\mathbf{x}\]

where \(m(\mathbf{x})\) represents the source distribution at every location in the subsurface (and effectively parametrises the source strength), \(G(\mathbf{x_r}, \mathbf{x}, t)\) is the subsurface-to-receiver Green’s function and finally \(w(t)\) is the source wavelet. In our implementation, the following high-frequency approximation of the Green’s function is adopted:

\[G(\mathbf{x_r}, \mathbf{x}, \omega) = a(\mathbf{x_r}, \mathbf{x}) e^{j \omega t(\mathbf{x_r}, \mathbf{x})}\]

where \(t(\mathbf{x_r}, \mathbf{x})\) is the traveltime and \(a(\mathbf{x_r}, \mathbf{x})\) is the amplitude. However, we currently discard the amplitude component.

In this tutorial we will consider a simple scenario where the subsurface is homogenous, as such we can compute an analytical expression for the traveltime. Similarly, an eikonal solver can also be used in this scenario as well as in more complex cases when we deal with heterogenous media.

import os
import numpy as np
import matplotlib.pyplot as plt

from pylops.utils import dottest
from pylops.utils.wavelets import ricker

import fracspy

from fracspy.visualisation.eventimages import locimage3d
from fracspy.utils.sofiutils import read_seis
# sphinx_gallery_thumbnail_number = 7

Load model and seismic data

For this example, we will use a toy homogenous model with a gridded surface receiver array. The data are modelled using the SOFI3D Finite Difference modelling software. The model is the same that we have used in the FD modelling to generate the data. As such, it contains additional boundaries, which we need to remove prior to performing localisation.

# Directory containing input data
input_dir = '../data/pyfrac_SOFIModelling'

# Model parameters
abs_bounds = 30
dx = dy = dz = 5
nx = 112
ny = 128
nz = 120

# Modelling parameters
dt = 1e-3  # SOFI3D Time sampling rate
t_shift = 167  # Time shift required to align FD data to zero time for Kirchhoff operators

# Load model
mod_w_bounds = np.fromfile(os.path.join(input_dir,'inputs',
                                        'models',
                                        'Homogeneous_xyz.vp'),
                           dtype='float32').reshape([nx, ny, nz])

# Load receiver geometry
recs_xzy = np.loadtxt(os.path.join(input_dir,'inputs',
                                   'griddedarray_xzy_20m.dat')).T
nr = recs_xzy.shape[1]

# Load seismic data
expname = 'explosive_Homogeneous_griddedarray'
vz = read_seis(os.path.join(input_dir, 'outputs',
                            'su', f'{expname}_vy.txt'),
               nr=nr)
vz = vz[:, t_shift:]  # Cut time axis to account for selected ignition time
vz /= np.max(abs(vz))  # Normalise to get reasonable amplitudes

# Remove absorbing boundaries from both the model and receiver coordinates
mod = mod_w_bounds[abs_bounds:-abs_bounds, abs_bounds:-abs_bounds, :-abs_bounds] # z has free surface
nx, ny, nz = mod.shape
x, y, z = np.arange(nx) * dx, np.arange(ny) * dy, np.arange(nz) * dz
recs = np.array([recs_xzy[0]-(abs_bounds*dx), recs_xzy[2]-(abs_bounds*dx), recs_xzy[1]])

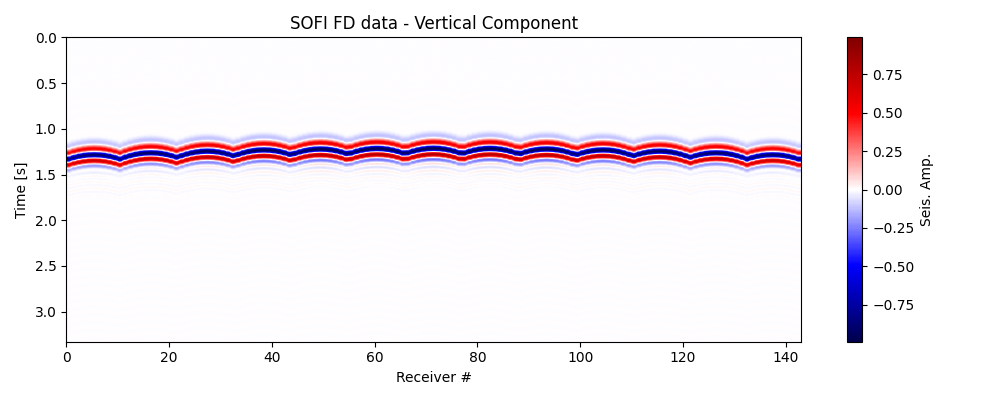
Let’s now double-check that the data has been loaded correctly.

fig, ax = fracspy.visualisation.traceviz.traceimage(vz, climQ=99.99, figsize=(10, 4))
ax.set_title('SOFI FD data - Vertical Component')
plt.tight_layout()

Create modelling operator

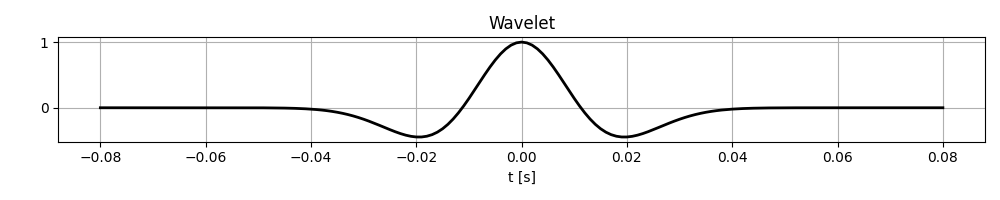
First, we will define a Ricker wavelet with peak frequency of 20Hz. This is the same wavelet that we used in modelling; in real applications, this will need to be estimated from the data.

nt = vz.shape[1]
t = np.arange(nt) * dt
wav, wavt, wavc = ricker(t[:81], f0=20)

fig, ax = plt.subplots(figsize=(10, 2))
ax.plot(wavt, wav, 'k', lw=2)
ax.set_xlabel('t [s]')
ax.set_title('Wavelet')
ax.grid('on')
plt.tight_layout()

Second, we define our modelling operator; as part of the initialization process, an eikonal solver is used here to compute the traveltimes from each subsurface point to each receiver.

Op = fracspy.modelling.kirchhoff.Kirchhoff(
        z=z,
        x=x,
        y=y,
        t=t,
        recs=recs,
        vel=1000 * np.ones_like(mod),
        wav=wav,
        wavcenter=wavc,
        mode='eikonal',
        engine='numba')

# Check operator with dottest
_ = dottest(Op, verb=True)

Dot test passed, v^H(Opu)=-5710.095725025381 - u^H(Op^Hv)=-5710.095725025408

ASIDE: Checking operator optimality

Here we will just forward model the data to check that it looks similar to the one computed via Finite-Difference. This is not strictly required if we are simply interested to apply the adjoint of our modelling operator (i.e., source localisation by imaging); however, it becomes important if we want to invert the modelling operator (i.e., source localisation by inversion). For such a simple subsurface model and synthetically generated data, we expect to have a good match even though our modelling operator is clearly ignoring some physics (e.g., geometrical spreading).

When working with field data, this preliminary step becomes even more important as one may want to look at the waveform to ensure that its kinematic and frequency content is consistent with that of the observed data. As far as the kinematic part is concerned, this will be dependant on the velocity model as well as the choice of the ignition time. [More commentary on ignition time can be found in the tutorial on rolling detection.]

# Choose a microseismic source location as function of grid points
sx = nx // 2
sy = ny // 2
sz = 2 * nz // 3
print(f'True source location [index]: {sx}-{sy}-{sz}')

microseismic = np.zeros((nx, ny, nz))
microseismic[sx, sy, sz] = 1.

# Perform forward modelling
frwddata_1d = Op @ microseismic.flatten().squeeze()
frwddata  = frwddata_1d.reshape(nr,nt)

True source location [index]: 26-34-60

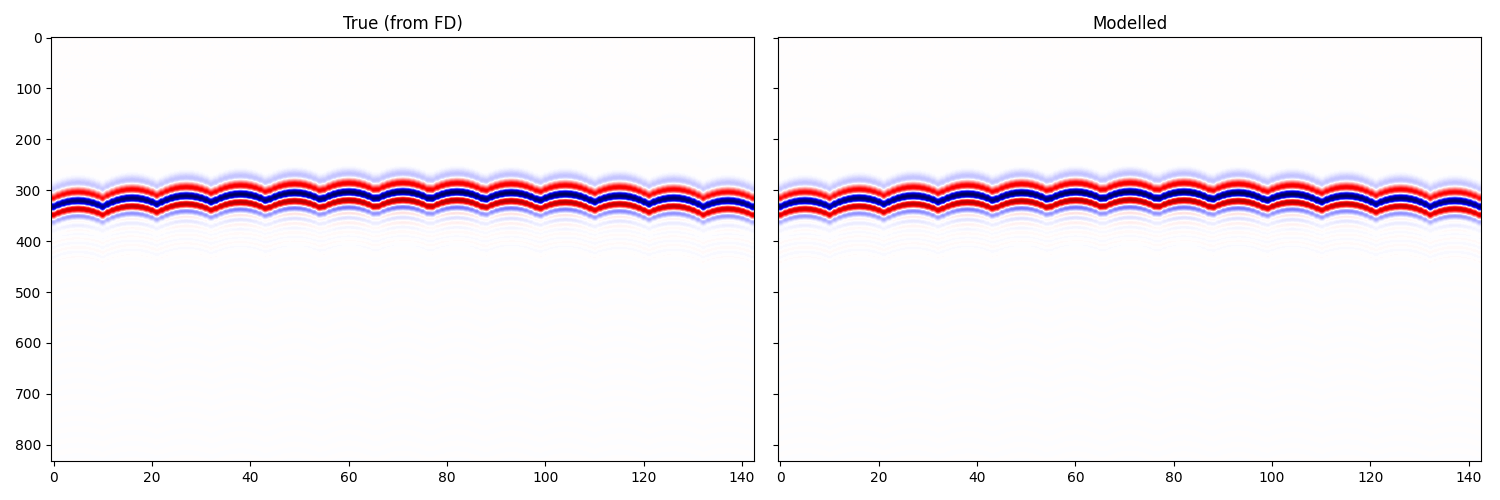
Let’s compare the data across the full array

fig, axs = plt.subplots(1, 2, sharey=True, figsize=[15,5])
axs[0].imshow(vz.T, aspect='auto', cmap='seismic', vmin=-1,vmax=1)
axs[0].set_title('True (from FD)')
axs[1].imshow(frwddata.T, aspect='auto', cmap='seismic', vmin=-1, vmax=1)
axs[1].imshow(vz.T, aspect='auto', cmap='seismic', vmin=-1,vmax=1)
axs[1].set_title('Modelled')
plt.tight_layout()

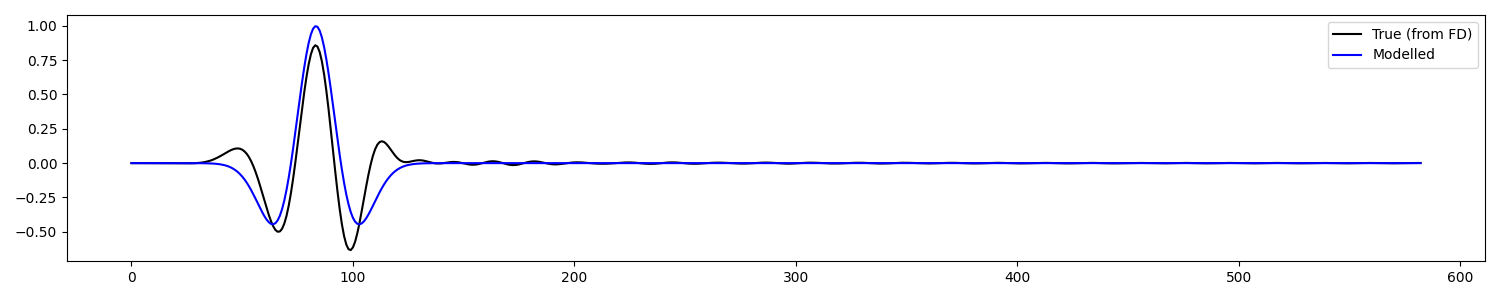
And at trace level

plt.figure(figsize=[15, 3])
plt.plot(-1 * vz[10, 250:], 'k', label='True (from FD)')
plt.plot(frwddata[10, 250:], 'b', label='Modelled')
plt.legend()
plt.tight_layout()

Source localisation by imaging

Creating an image of our microseismic source using the adjoint of the modelling operator is a good first step to assess its ability to relocate the energy of the event of interest to a certain subsurface location.

In our setup, the adjoint is fast to perform. Therefore, we recommend computing the adjoint to gain an initial idea on possible source locations. However, the source location is likely to be a smoothed product, as opposed # to the desired single location.

L = fracspy.location.Location(x, y, z)
migrated, mig_hc = L.apply(vz, kind="kmigration", Op=Op, nforhc=10)

print('True Hypo-Center:', [sx,sy,sz])
print('Migration Hypo-Centers:', mig_hc)

clim = np.max(abs(migrated))
fig, axs = locimage3d(migrated,
                      x0=int(np.round(mig_hc[0])),
                      y0=int(np.round(mig_hc[1])),
                      z0=int(np.round(mig_hc[2])),
                      clipval=[-clim, clim])
plt.tight_layout()

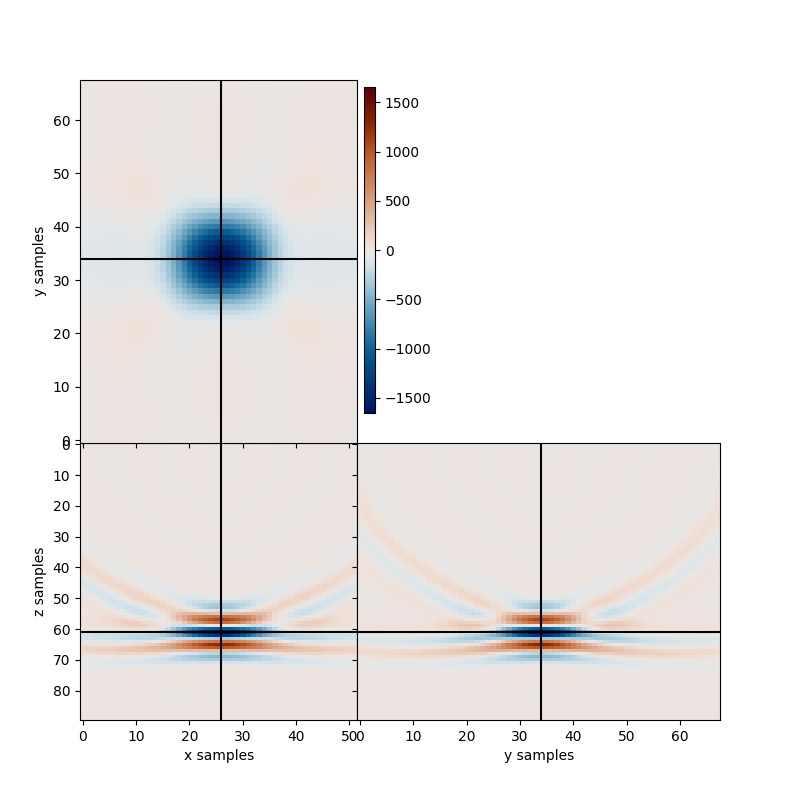
True Hypo-Center: [26, 34, 60]
Migration Hypo-Centers: [26.2 34.  61. ]

Source localisation by inversion

We try now to fully invert the forward operator. Two approaches will be explored: first, we consider a standard least-squares solution, followed by a sparsity-promoting inversion with the FISTA solver. The former approach is likely to share some of the downsides of the adjoint solution unless inversion is carried out usig a very large number of iterations. However, since the modelling operator is not exact, it may become unstable as iterations progress. On the other hand, adding a sparsity constraints can lead to a better resolved source location. Note, however, that in both cases error in the velocity model cannot be compensated and will contribute to the blurring of the resulting source image.

Let’s start with the least-squares solution

inv, inv_hc = L.apply(vz, kind="lsi", Op=Op,
                      nforhc=10, verbose=False)

print('True Hypo-Center:', [sx,sy,sz])
print('LSQR Inversion Hypo-Centers:', inv_hc)


clim = np.max(abs(inv))
fig,axs = locimage3d(abs(inv),
                     x0=int(np.round(inv_hc[0])),
                     y0=int(np.round(inv_hc[1])),
                     z0=int(np.round(inv_hc[2])),
                     clipval=[-clim, clim])
plt.tight_layout()

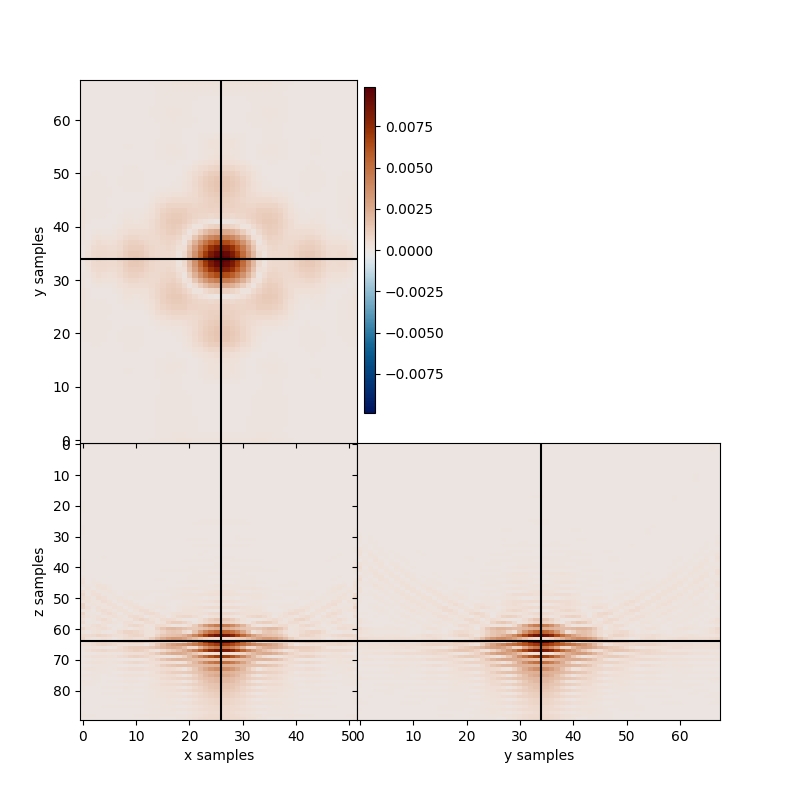
True Hypo-Center: [26, 34, 60]
LSQR Inversion Hypo-Centers: [26.  34.  63.8]

We move on now to the sparsity-promoting solution

fista, fista_hc = L.apply(frwddata, kind="sparselsi", Op=Op,
                          l1eps=1e1, nforhc=10, verbose=False)

print('True Hypo-Center:', [sx, sy, sz])
print('FISTA Inversion Hypo-Centers:', fista_hc)

clim = np.max(abs(fista))
fig, axs = locimage3d(abs(fista),
                      x0=int(np.round(fista_hc[0])),
                      y0=int(np.round(fista_hc[1])),
                      z0=int(np.round(fista_hc[2])),
                      clipval=[-clim, clim])
plt.tight_layout()

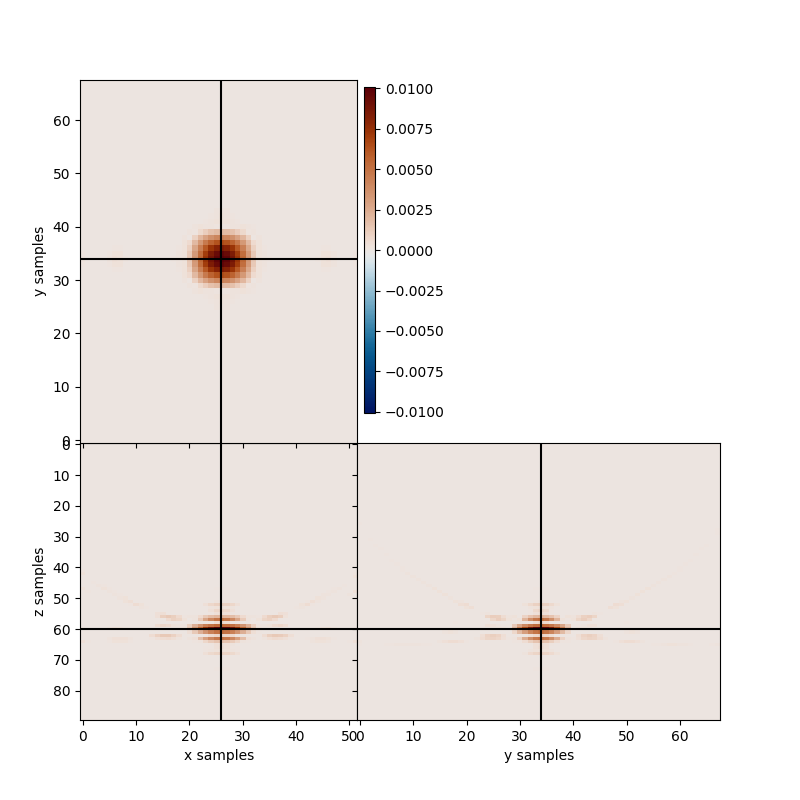
True Hypo-Center: [26, 34, 60]
FISTA Inversion Hypo-Centers: [25.8 34.  60. ]